正则表达式 - 匹配原理及ReDoS攻击
有穷自动机
在计算机科学理论中,采用 计算模型的理想计算机 来建立数学理论,其中 有穷自动机 就是其中之一,除此之外还有,图灵机、递归函数、λ演算、马尔科夫算法等。
有穷自动机(Finite Automata,也叫有穷状态自动机,finite-state machine)。
理解有穷自动机
例如:自动售卖机就是一种有穷自动机。假设自动售卖机只接收面额为5元的纸币。当你塞入一张5元购买3元的饮料时,机器会给你饮料及找回的2元零钱。
有穷自动机必须满足4个条件:
- 具有有限多个状态。(根据找零余额的不同,可能有的状态为6个:5元、4元、3元、2元、1元、0元)
- 有一套状态转移函数。(比如余额还有3元,你买了一瓶2元的饮料,则转移到状态“1元”,如果你选择买4元的饮料,则报告“余额不足”,状态并不变化)
- 有一个开始状态。(余额5元)
- 有一个或多个最终状态。(余额0元)
自动售货机并不关心买了什么商品,也不关心选择商品的顺序,无论做什么,它总处在这6个状态之一,只需要根据 状态转移函数 在其中转移即可。
典型应用
Regular Expression 正则表达式
Lexical Analyzing 词法分析
Pattern Matching 模式匹配
精确匹配,前缀匹配
多模式匹配(AC自动机)
Dictionary Compressing 词表压缩
- 自动机最小化,字典序计算
正则引擎的分类
正则表达式所使用的理论模型就是有穷自动机。
正则引擎(Regex Engine)主要分为两大类:
DFA(Deterministic Finite Automaton,确定有穷自动机)和NFA(Nondeterministic Finite Automaton,非确定有穷自动机)NFA 有 传统型NFA(Traditional NFA)和 POSIX NFA两种。两者的主要区别在于,如果多选分支中的多个分支都能匹配,传统型的NFA优先选择左侧的分支,而POSIX NFA一定要选择最长的分支。如匹配字符串
Tomcat,若正则为(Tom|Tomcat),传统型NFA结果为Tom,POSIX NFA结果为Tomcat;若正则为(Tomcat|Tom),传统型NFA结果为Tomcat,POSIX NFA结果为Tomcat。
常用程序所使用的正则引擎
| 引擎类型 | 程序 |
|---|---|
| DFA | awk(大多数版本)、egrep(大多数版本)、MySQL |
| 传统型NFA | grep(大多数版本)、Perl、.NET、Java、JavaScript、PHP、Python、Ruby、vi |
判断 传统型NFA 还是 POSIX NFA
匹配字符串
Tomcat,若正则为(Tom|Tomcat),传统型NFA结果为Tom,POSIX NFA结果为Tomcat;若正则为(Tomcat|Tom),传统型NFA结果为Tomcat,POSIX NFA结果为Tomcat。
判断 DFA 还是 POSIX NFA
DFA不支持捕获型括号(capturing parentheses)和 回溯(backreferences)。
不过,也存在同时使用两种引擎的混合系统,如果没用使用捕获型括号,就会使用DFA。
用正则
^(a+)+$,测试文本aaaaaaaaaaaaaaaaaaaaax:
- 如果执行时间很短,为DFA
- 如果执行时间很长,为NFA(再用上一项判断方法,进一步判断是传统型NFA 还是 POSIX NFA)
- 如果堆栈溢出(stack overflow)或超时退出,为NFA。
DFA 和 NFA 比较
- 文本主导的DFA引擎 比 表达式主导的NFA引擎 要快。因为DFA引擎是 确定型的(deterministic),目标文本中的每个字符仅检查一遍。
- DFA不需要回溯,即不需要保存状态。
- 在构建复杂的正则(多选分支)时,DFA需要更多的时间和内存。因为开始尝试匹配的时候,它已经内建了一张路线图(map),字符串中每个字符都会按照这张路线图来匹配。
正则的匹配过程
DFA引擎
用正则
a(d|b)c匹配文本abc的匹配过程
| 步骤 | 字符串 | 正则 |
|---|---|---|
| 1.编译正则,准备开始匹配 | abc | a(d|b)c |
2.匹配 a,匹配成功 |
abc | a(d|b)c |
3.下一个字符,b 匹配成功 |
abc | a(d|b)c |
4.下一个字符,c 匹配成功 |
abc | a(d|b)c |
5.匹配结束,结果为 abc |
abc | a(d|b)c |
DFA引擎的一些特点:
- 文本主导:按照文本的顺序执行,这也就能说明为什么DFA引擎是确定型(deterministic)了,稳定!
- 记录当前有效的所有可能:我们看到当执行到
(d|b)时,同时比较表达式中的d和b,所以会需要更多的内存。- 每个字符只检查一次:这提高了执行效率,而且速度与正则表达式无关。
- 不能使用反向引用等功能:因为每个字符只检查一次,文本零宽度(位置)只记录当前比较值,所以不能使用反向引用、环视等一些功能!
NFA引擎
用正则
a(d|b)c匹配文本abc的匹配过程
| 步骤 | 字符串 | 正则 |
|---|---|---|
| 1.编译正则,准备开始匹配 | abc | a(d|b)c |
2.匹配 a,匹配成功 |
abc | a(d|b)c |
| 3.从正则分支中,选择左边的匹配 | abc | a(d|b)c |
| 4.记录当前位置(备用状态,saved state) | a_bc | a(d|b)c |
5. d 匹配不成功 |
a_b_c | a(d|b)c |
| 6.换另外一个分支匹配,位置回退 | a_bc | a(d|b)c |
7.重新传动,b 匹配成功 |
a_b_c | a(d|b)c |
8.下一个字符,c 匹配成功 |
abc | a(d|b)c |
9.匹配结束,结果为 abc |
abc | a(d|b)c |
NFA引擎的一些特点:
- 文表达式主导:按照表达式的一部分执行,如果不匹配换其他部分继续匹配,直到表达式匹配完成。
- 会记录某个位置:我们看到当执行到
(d|b)时,NFA引擎会记录字符的位置(零宽度),然后选择其中一个先匹配。- 单个字符可能检查多次:我们看到当执行到
(d|b)时,比较d后发现不匹配,于是NFA引擎换表达式的另一个分支b,同时文本位置回退,重新匹配字符’b’。这也是NFA引擎是非确定型的原因,同时带来另一个问题效率可能没有DFA引擎高。- 可实现反向引用等功能:因为具有回退这一步,所以可以很容易的实现反向引用、环视等一些功能!
注意:**绝大多数编程语言都选择 NFA (非确定型有穷自动机) 作为引擎 **
回溯
当正则匹配不成功之后,文本的位置发生回退,选择另外一个分支匹配的这个回退操作,叫做 回溯 。
回溯的原理 类似走迷宫。当遇到死胡同的时候需要返回原来的位置后,再进入新的道路。
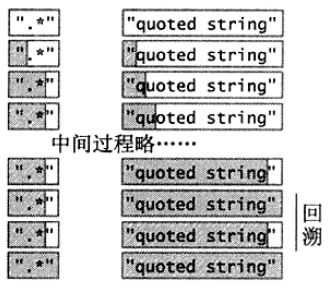
例子
- 正则
".*"针对"quoted string"的匹配过程
- 正则
".*"针对"quoted" string的匹配过程
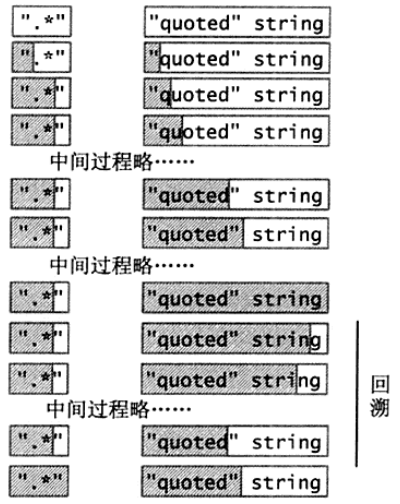
例子1中,.* 匹配了 quoted string" 后,因为要保证正则中最后一个" 的匹配,不得不回溯一次;
例子2中的回溯成本要大于例子1,避免这类问题,最好的办法是 准确的表达意图。
优化例子2(可以访问 regex101 进行debug观察执行过程):
- 规定双引号字符串中不能出现双引号字符,
"[^"]*" - 换用忽略量词,
".*?" - 除非确实必要,尽量不使用
.* - 绝对避免出现
(……*)*结构的正则。这个时候的回溯会呈指数级增长!!
在实际应用中,除了注意自己写的正则,还需要防范来自外界的恶意程序,它们会造成大量回溯,讲CPU资源消耗殆尽。
这种攻击叫做,正则表达式拒绝服务攻击(Regular Expression Denial of Service)
ReDoS攻击
计算(回溯)
计算机在处理正则表达式的时候可以说是非常愚蠢,虽然看上去它们有很强的计算能力。当你需要用 x*y 表达式对字符串 xxxxxxxxxxxxxx 进行匹配时,任何人都可以迅速告诉你无匹配结果,因为这个字符串不包含字符y。但是计算机的正则表达式引擎并不知道!它将执行以下操作
xxxxxxxxxxxxxx # 不匹配
xxxxxxxxxxxxxx # 回溯
xxxxxxxxxxxxx # 不匹配
xxxxxxxxxxxxx # 回溯
xxxxxxxxxxxx # 不匹配
xxxxxxxxxxxx # 回溯
xxxxxxxxxxx # 不匹配
xxxxxxxxxxx # 回溯
>>很多很多步骤
xx # 不匹配
x # 回溯
x # 不匹配
# 无匹配结果
你不会以为结束了吧?这只是第一步!
现在,正则表达式引擎将从第二个x开始匹配,然后是第三个,然后是第四个,依此类推到第14个x。
最终总步骤数为256。它总共需要256步才能得出无匹配结果这一结论。计算机在这方面真的很蠢。
同样,如果你使用非贪婪匹配,x*?y 表达式会从一个字母开始匹配,直到尝试过所有的可能,这和贪婪匹配一样愚蠢。
利用
正如之前所见,使用正则表达式进行匹配搜索可能需要计算执行大量计算步骤,但一般来说这并不是问题,因为计算机速度很快,并且可以在眨眼间完成数千个步骤。
但是,计算机也是有极限的,我们能否造出一个字符串让计算机长时间的超负荷运转?
重复运算符嵌套
如果你看到一个重复运算符嵌套于另一个重复运算符,就可能存在问题。
表达式: xxxxxxxxxx 17945(x+)*y
Motive: 会匹配任意数量的x加上一个y
匹配字符串: xxxxxxxxxx(10 chars)
计算步骤数: 17945此时计算步骤数并不算多,但是,这个增长趋势是很惊人的。
字符串 X的个数 步数
z 0 3
xz 1 6
xxz 2 19
xxxz 3 49
xxxxz 4 122
xxxxxz 5 292
xxxxxxz 6 687
xxxxxxxz 7 1585
xxxxxxxxz 8 3604
xxxxxxxxxz 9 8086
xxxxxxxxxxz 10 17945
xxxxxxxxxxxz 11 39451
xxxxxxxxxxxxz 12 86046
xxxxxxxxxxxxxz 13 186400
xxxxxxxxxxxxxxz 14 401443
xxxxxxxxxxxxxxxz 15 860197
xxxxxxxxxxxxxxxxz 16 1835048
xxxxxxxxxxxxxxxxxz 17 3899434
xxxxxxxxxxxxxxxxxxz 18 8257581
xxxxxxxxxxxxxxxxxxxz 19 17432623
xxxxxxxxxxxxxxxxxxxxz 20 36700210
xxxxxxxxxxxxxxxxxxxxxz 21 77070388如上所见,计算步骤数随着输入字符串中X的数量呈指数增长。
我不是很擅长数学,但如果输入40个x,貌似需要的计算步骤数是:
计算步骤数 = 98516241848729725
如果计算机可以在1秒内完成100万个计算步骤,则需要3123年才能完成所有计算。
以上我们所展示的情况看起来很是糟糕,但是还存在其他糟糕的情况。
多个重复运算符1
如果两个重复运算符相邻,那么也有可能很脆弱。
表达式: .*\d+\.jpg
Motive: 会匹配任意字符加上数字加上.jpg
匹配字符串: 1111111111111111111111111 (25 chars)
计算步骤数: 9187它没有前一个那么严重,但如果程序没有控制输入的长度,它也足够致命。
多个重复运算符2
如果两个重复运算符较为相近,也有可能受到攻击。
表达式: .*\d+.*a
Motive: 会匹配任意字符串加上数字加上任意字符串加上a字符
匹配字符串: 1111111111111111111111111 (25 chars)
计算步骤数: 77600多个重复运算符3
|符号加上[]符号再配上+也可能受到攻击。
表达式: (\d+|[1A])+z
Motive: 会匹配任意数字或任意(1或A)字符串加上字符z
匹配字符串: 111111111 (10 chars)
计算步骤数: 46342ReDoS检测
- RegexStaticAnalysis工具,项目地址:https://github.com/NicolaasWeideman/RegexStaticAnalysis
- RegexFuzzer(微软),SDL Regex Fuzzer https://download.cnet.com/SDL-Regex-Fuzzer/3000-2383_4-75321803.html
- 正则表达式在线测试网站,网址:https://regex101.com/
附录
有穷自动机
概述
有穷自动机有一组状态及其控制,响应外部的“输入”,“控制”从状态移动到状态。各类有穷自动机之间的关键区别之一,在于控制究竟是“确定的”还是“非确定的”,前者意味着在任何时候自动机不能处在一种以上的状态中,后者意味着自动机能同时储在几种状态中。
确定型有穷自动机(DFA)

通常同一个五元组来讨论DFA:
A=(Q,Σ,δ,q0,F)
其中A表示DFA的名称,Q是状态集合,Σ是输入符号的集合,δ是转移函数,q0是初始状态,F是接收状态的集合。
例:
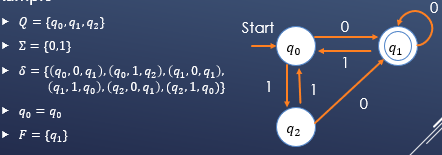
其中同心圆表示的是终止状态
确定的有限自动机的转换表表示法:

其中“→”符号标记的是起始状态,“*”标记的是终止状态。
DFA的扩展转移函数

DFA接受的语言

需要注意的是,有限状态自动机每种状态下接受的输入应该考虑到每一种可能的符号,即使实际的语言并不会在某种状态下产生某个符号,也应该设计一个死锁来接受该种符号。
下例中,状态D就是一种死锁状态:
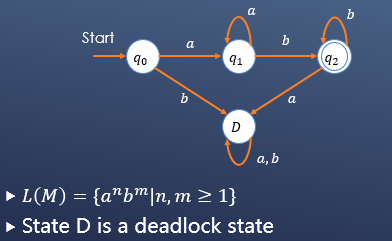
设计能接受某种语言的自动机时,第一步应该考虑的直接从起始状态进入终止状态的情况,然后依次考虑每种状态能进入终止状态的情况。
不确定的有限状态自动机(NFA)

这里的2Q表示Q的幂集
例如:

也就是说,不确定有限状态自动机中的一个状态接收同一个输入可能会跳转到不同的状态,并且支持跳转空状态。
NFA的扩展转移函数

可以发现,DFA的扩展转移函数和NFA的扩展转移函数的区别在于:DFA的扩展转移函数的右边是一个确定的状态,而NFA的扩展转移函数的右边是一个状态的集合,而这个集合种可以有多个状态也可以是一个空集。
NFA接受的语言
例如:
通过子集构造将NFA转化成DFA
当将NFA转化成DFA的时候,DFA的状态转移函数的右边是一个集合,不过这依然是一个确定的状态,它是这样的一个状态:由NFA的状态集合而构成的一个确定的状态。换句话说,DFA的状态集合是NFA的状态集合的子集的集合。
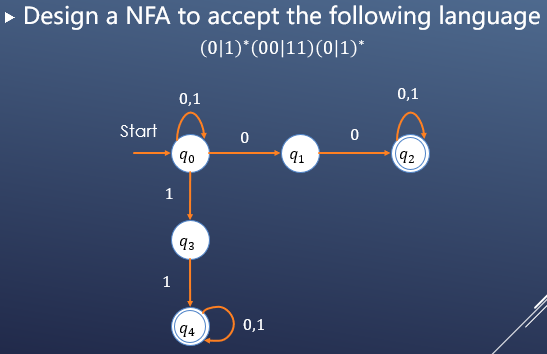
下图是一个NFA的状态迁移图:
子集构造:

然后根据上述的子集构造方法构造NFA的完整子集构造。因为NFA有3种状态{q0, q1, q2},所以完整的子集构造产生一个带有23=8种状态的DFA,对应于这三种状态的所有子集合。下图是这8中状态的状态转移表。

显然,对于上面这8种状态,从状态{q0}开始,只能到达{q0}、{q0, q1}、和{q0, q2}。其余5种状态都是从初始状态不可达的,也都可以不出现在表中。
进行了子集构造后,去除多余的状态即可得到这样的一个DFA,它与上面的NFA等价:
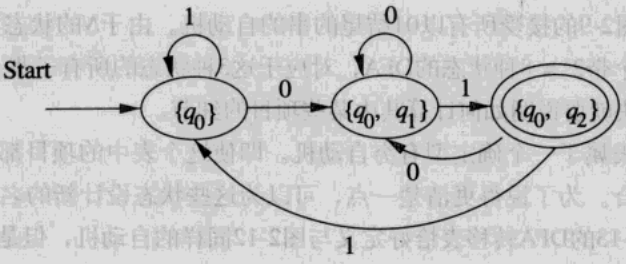
带空迁移的有限自动机(ε-NFA)

例如:
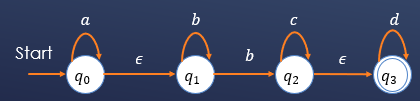
也就是说,带空迁移的有限状态自动机支持输入空符号进行状态迁移。
ε闭包
非形式化的定义:顺着所有从状态q出发带ε标记的转移来求状态q的ε的闭包。但当顺着ε到达其他状态后,再从这些状态发出ε转移,依此类推,最终求出顺着箭弧都带ε标记的任何路径从q可达的任何每个状态。
而其形式化的定义如下:

ε-NFA的扩展转移

ε-NFA接受的语言
与NFA一样,如果一个语言产生的句子中存在一条能从起始状态到达终止状态的路径,则称这种语言是ε-NFA接受的语言,记为:
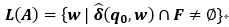
显然,ε-NFA和NFA是等价的。对于一个ε-NFA,依次讨论每种状态下接收非空符号的状态迁移情况,可以构造出一个NFA。